Diophantine-based encryption

The advent of quantum computers has threatened existing encryption algorithms based on factorization and discrete logarithm problems. This encourages the search for new mathematical problems that are resistant to quantum powers.

According to the works of K. Shannon, there is no algorithm that allows one to determine the solution of an arbitrary Diophantine equation. Cryptographic systems based on such equations for an illegal user reduce the ability to reduce the set of searched keys and, therefore, require an unlimited amount of computational work and resources when cracking.

What is diophantine equations?

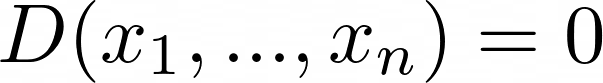
D is a polynomial with integer coefficients, x1, …, xn are unknown variables of equation. It should be noted that x1, …, xn ∈ Z, i.e. only whole numbers are considered solutions.

Note that the problem of solving equations in integers has been completely solved only for equations with one unknown, for equations of the first degree, and for equations of the second degree with two unknowns. For equations above the second degree with two or more unknowns, even the problem of determining the existence of integer solutions is quite difficult.

Usage in cryptosystem

Let us compose a mathematical model of a symmetric bigram cryptosystem, i.e. cryptosystem in which the text is divided into blocks of 2 elements — digrams, and one secret key is used for encryption and decryption.

As a basis for the algorithm, we use a linear Diophantine equation of the 1st degree:

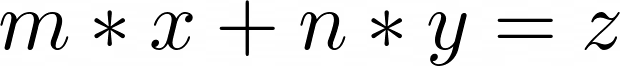
Where x, y∈N; m,n,z ∈Z

Where m and n are arbitrary integers, and x and y are variables. It is known that for the case when gcd(m, n) = 1, equation has the following entire parametric solutions:

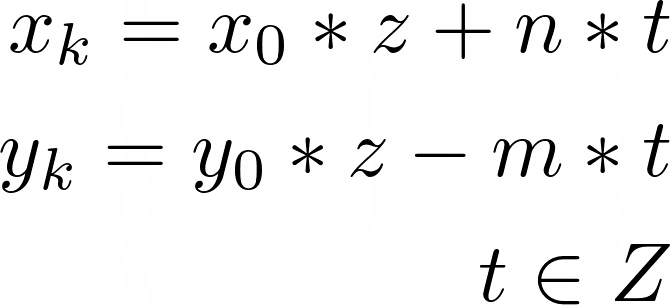
Where x0, y0 is an integer solution of the equation mx+ny=1

To ensure the uniqueness of the solution of this problem by a legal user, we use a system of linear Diophantine equations:

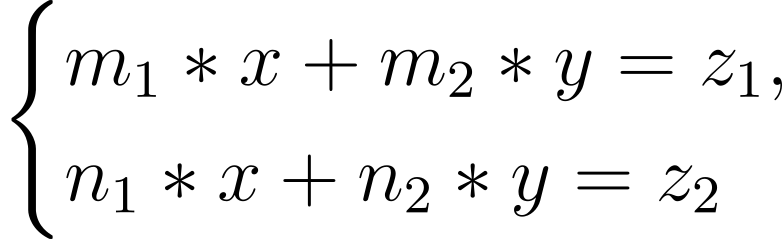
Where x, y∈N; mi,ni, zi ∈ Z, m and n are arbitrary integers and x and y are variables.

For the secret key, we take pairs of numbers (m1, n1) and (m2, n2) — the coefficients of the system. Suppose that (x, y) are known numerical equivalents of some digram. Then, substituting the indicated values into system, we obtain a pair of numbers (z1, z2) — encrypted numerical equivalents of this digram.

After receiving the encrypted data, the legal user will know all the coefficients of the system of 2 linear Diophantine equations with 2 unknowns. For this system, the Kronecker-Cappelli theorem is satisfied, i.e. the system is consistent and has a unique solution.

Example

Suppose user A needs to send user B an encrypted bigram M = (3, 9). The secret key will consist of two pairs of coprime numbers v = (m1, n1, m2, n2). Specifically, for this example, we will choose the key v = (17, 3, 13, 21).

User A substitutes the secret key and numerical equivalents of the bigram into system and receives the vector z = (z1, z2), which is the encrypted bigram. In our case, the vector z = (511, 483), which is then transmitted over the channel.

During the decryption process, user B substitutes the vector z and the secret key v into system and receives a simple system of linear Diophantine equations, in our case:

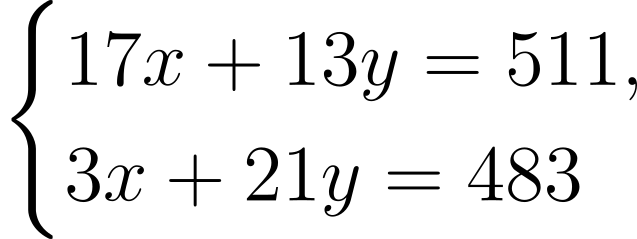
Solving the resulting system, B uniquely determines the numerical equivalents of x and y: x=3, y=9.

An illegal user who managed to intercept the vector z is faced with the task of solving a system of linear Diophantine equations. Since the number of unknowns exceeds the number of equations themselves, the problem has infinitely many solutions.

Scientific article from the 2021 conference is available here: https://hiddenproject.tech/ru/science/diophantine_models_for_encryption.pdf