Диофантовые модели в криптографии

Появление квантовых компьютеров угрожает существующим алгоритмам шифрования на основе задач факторизации и дискретного логарифмирования. Это заставляет криптографию искать новые математические методы и модели для защиты информации в пост-квантовой эре, устойчивые к успехам технического прогресса.

Согласно работам К. Шеннона не существует алгоритма, позволяющего определить решение произвольного диофантова уравнения. Криптографические системы на основе таких уравнений для нелегального пользователя сокращают возможность уменьшить множество перебираемых ключей и, следовательно, потребуют неограниченного объема вычислительной работы и ресурсов при взломе.

Определение диофантова уравнения?

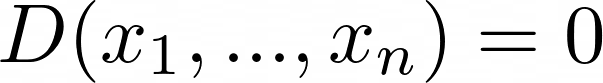
Где D — полином с целыми коэффициентами, x1, …, xn неизвестные переменные уравнения. Стоит отметить, что x1, …, xn ∈ Z, т.е. решениями считаются только целые числа.

Отметим, что проблема решения уравнений в целых числах решена до конца только для уравнений с одним неизвестным, для уравнений первой степени и для уравнений второй степени с двумя неизвестными. Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже задача определения существования целочисленных решений.

Использование в криптосистемах

Составим математическую модель симметричной биграммной криптосистемы, т.е. криптосистемы, в которой текст разбивается на блоки из 2 элементов – биграммы, а для шифрования и дешифрования используется один секретный ключ.

В качестве основы для алгоритма используем линейное диофантово уравнение 1-й степени:

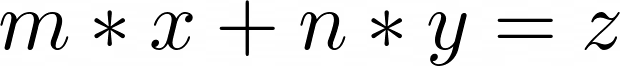
Где x, y∈N; m,n,z ∈Z, m и n — произвольные целые числа, а x и y — переменные. IИзвестно, что для случая, когда НОД(m, n) = 1, уравнение имеет следующие целые параметрические решения:

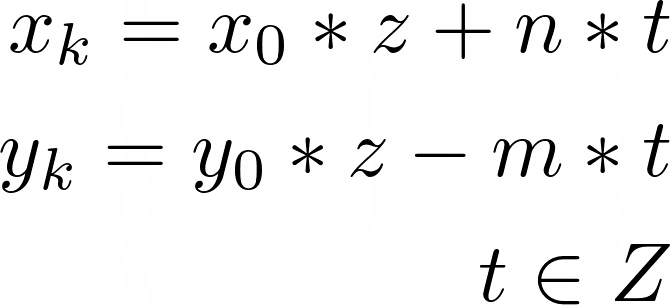
Где x0, y0 — целое решение уравнения mx+ny=1

Для обеспечения единственности решения данной задачи легальным пользователем используем систему линейных диофантовых уравнений:

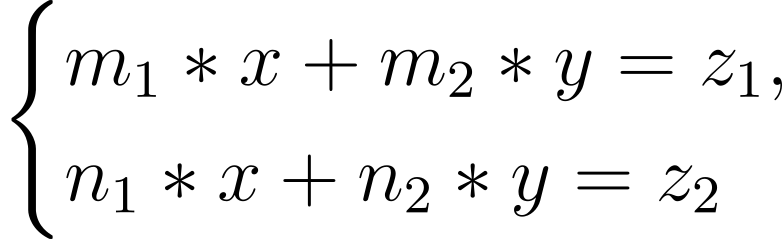
Где x, y∈N; mi,ni, zi ∈ Z, m и n — произвольные целые числа, а x и y — переменные.

За секретный ключ примем пары чисел (m1, n1) и (m2, n2) — коэффициенты системы. Предположим, что (x, y) — известные числовые эквиваленты некоторой биграммы. Тогда, подставляя указанные значения в систему, получим пару чисел (z1, z2) — зашифрованные числовые эквиваленты этой биграммы.

После получения зашифрованных данных легальному пользователю будут известны все коэффициенты системы из 2 линейных диофантовых уравнений с 2 неизвестными. Для этой системы выполняется теорема Кронекера – Капелли, т.е. система совместна и имеет единственное решение.

Пример

Предположим, пользователю А необходимо отправить пользователю Б зашифрованную биграмму M = (3, 9). Секретный ключ составят две пары взаимно простых чисел v = (m1, n1, m2, n2). Конкретно, для данного примера выберем ключ v = (17, 3, 13, 21).

Пользователь А подставляет секретный ключ и числовые эквиваленты биграммы в систему и получает вектор z = (z1, z2), который и является зашифрованной биграммой. В нашем случае вектор z = (511, 483), который затем передаем по каналу.

В процессе дешифрования пользователь Б подставляет вектор z и секретный ключ v в систему и получает простую систему линейных диофантовых уравнений, в нашем случае:

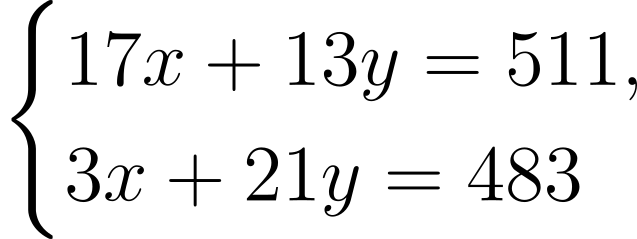
Решая полученную систему Б однозначно определяет числовые эквиваленты x и y: x=3, y=9.

Перед нелегальным пользователем, которому удалось перехватить вектор z, стоит задача решить систему линейных диофантовых уравнений. Так как количество неизвестных превышает количество самих уравнений, то задача имеет бесконечно много решений.

Научная статья с конференции 2021 доступна тут: https://hiddenproject.tech/ru/science/diophantine_models_for_encryption.pdf